Designing a TTRPG Combat System
In this post we will look at how to create a basic, turn-based D12 TTRPG combat rule system, using opposing/comparative rolls. We will be making use of the delta/difference between the attacker and the defender roll to have more nuanced grades of success - instead of just “hit” or “miss”. As usual for this blog, everything in this post is free to use under a CC BY 4.0 license.
Check out the previous post in this series, to learn more about comparative die rolls and deltas.
Most TTRPG systems are made for idealist/mythic/epic stories (including all of setting, characters and plot). But I am creating this one specifically to support a story that’s more realist/gritty/grounded. Check out my post Two Types of Story to learn more about this distinction.
D12 - are you mad? Why not use a D20 like everyone else?
Well, yes, I probably am, thank you for asking. But you can easily follow along and just replace my D12 with your D20, thus creating a D20 version of this. Shouldn’t be a problem.
I’ve been tinkering with this rule system on and off for many years now - and for most of the time, it actually was a D20 based system. But I ran into issues with the deltas on a D20 being just too large, and the percent chances of rolling high deltas getting too large as well. And with comparative rolls, there is no real need for that increased granularity in the first place. Using a D12 solves all those issues rather beautifully. It might of course cause other problems I’m not anticipating right now, forcing me to switch back to D20 after all. Who knows. But for now, a D12 system it is!
(I do have to admit though, I kinda like the idea of going for a D12 system, precisely because everyone else is doing D20. That really stands out, doesn’t it?)
Hit & Damage Calculations and Weapons
Assuming we have an attacker and a defender of completely equal strength and skill - then our hit calculation is purely an opposing die roll:
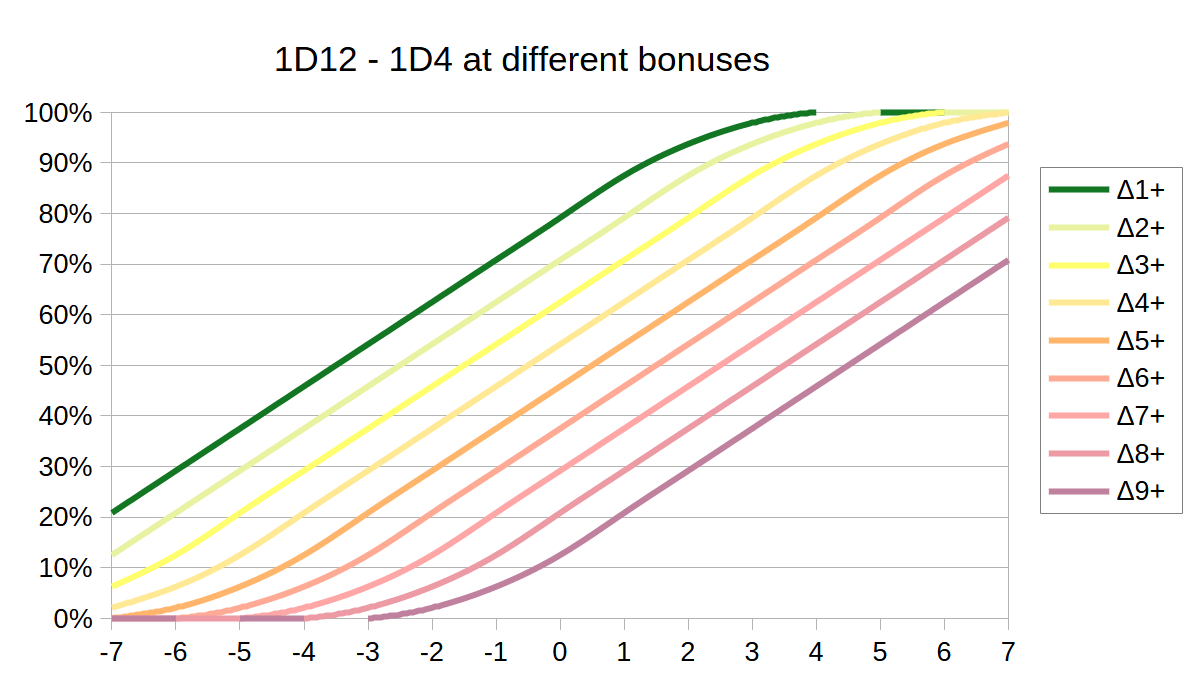
The attacker rolls a D12, the defender rolls a D12, and the difference of these two rolls 1D12 - 1D12 is a number, which we call the delta. So, if the attacker rolls a 9, and the defender rolls a 3 - we get a delta of 6. That means, (up to) 6 hits were landed successfully.
A sniper weapon that fires only one shot, would always do exactly one hit of damage (when it hits). An assault weapon that fires 5 shots might do anywhere from 1 to 5 hits of damage, depending on the delta. Assuming the sniper weapon deals 9 damage per hit, and the assault weapon does 4 damage per hit - and further assuming the enemy wears armor with a damage reduction value of 1 - then the sniper would always do 8 damage - while the assault would do anywhere from 3 to 15 damage, depending on how many hits are scored. If the enemy has armor with damage reduction 2, these values change to 7 damage for the sniper, and 2 to 10 damage for the assault.
As I am going for a sci-fi setting with pew-pew weapons, I’m only talking about ranged weapons here. But this can equally be applied to medieval swords and axes. A short sword or dagger would do multiple swings (or stabs) in a single attack - but a large, heavy, two-handed hammer would get only one single swing. The delta signifies how many of these swings/stabs do connect. The damage reduction of the armor then decides how much damage actually goes through. Works just as well.
This means that a sniper weapon that fires only one shot, reaches it’s full damage potential at a delta of 1 or more (Δ1+) - while an assault weapon that fires 5 shots will only reach it’s full potential at Δ5+ (=a delta of five or more), and will deal less damage on lower deltas. On average both weapons will deal roughly the same damage - but the sniper is a lot more efficient against hard-to-hit enemies, while the assault is a lot more efficient against easy-to-hit enemies. Simultaneously, the sniper is potentially stronger against heavily armored enemies, while the assault deals more damage against lower armor - but this effect is somewhat counteracted by the fact, that wearing heavier armor makes characters less evasive and thus easier to hit.
How hard or easy an opponent is to actually hit, will of course also depend on how strong and skilled they are. Having attackers and defenders of completely equal strength and skill is not common, after all.
Power Levels
We generally do want character progression in our roleplaying games. We want to earn XP and then get to spend points which allow us to make our character not only stronger - but also unique, individual, and specialized. We can have a character arc and character growth through roleplay - but generally we also want gamified growth through improving our character to make them stronger - increasing the power level.
The Challenges With That
- When spending XP on getting +1 to attack, that should be a noticeable improvement.
- Such +1s should be available every now and then, without excessive wait times in between.
- Characters should not hit a maximum very quickly, but be able to continue getting +1s over long time frames.
- We do not want chance to hit to ever become 100%, or 0%. And we prefer a more elegant, natural solution over a crutch like critical hits/misses to just barely avoid having 100% or 0% chances.
- We do not want hit points and damage output to grow so much we end up with one-hit-kills vs. negligible scratches.
- But we do want a clear and strong advantage for the higher level, more skilled fighter.
- We want strength in numbers. A significantly large group of lower level combatants should pose a real threat to a tiny group of higher level characters. An army should be an overwhelming force.
- We want to be able to have a more grounded setting and game world, where powers don’t grow to god-like proportions.
- We want visceral, deadly combat - not a slow chipping away of hit points.
- But we don’t want defeat to feel too random, too unpredictable. It should only be unpredictable for equal strength opponents.
But is that even possible? This feels like a “you can’t have it all” situation, where the best you can do is pick two out of three, or something like that. Can you give a character regular +1s over a long time, with a single +1 being a siginificant, noticeable improvement, but +30 or even +50 not being so overpowered it just completely trounces a +1 opponent?
This is where a D20 gives you more headroom over a D12. You reach 100%/0% only at +19/-20, whereas with a D12 you already run into that problem at just +11/-12. At the same time, the +5% chance improvement of a D20 is less noticable then the +8.3% improvement that comes with a D12.
That’s the reason why in D&D a situational bonus to your roll always gives you +2 rather than +1 - because those +10% chance make a noticeable difference, while those +5% don’t quite feel like they matter.
I think it is possible and have it all - but to get there, we first have to take…
A Closer Look At The Numbers
We are rolling a D12 against an opposing D12. That would be something along the lines of 1D12 > 1D12 - or if you add in attack bonus a and “armor class” b, then it becomes 1D12 + a > 1D12 + b. (Which is of course exactly the same as 1D12 + (a - b) > 1D12).
But we are intersted in the delta, in the actual difference between those rolls, which would be 1D12 - 1D12. If the attacker rolls an 8 and the defender rolls a 3, the resulting delta would be 5. If you add in attack bonus and armor class, you get (1D12 + a) - (1D12 + b). (Which again equals 1D12 + (a - b) - (1D12)).
If both sides are of equal strength, then a = b which cancels out, because (a - b) becomes 0. And then only 1D12 - 1D12 remains. But if the attacker is stronger, we expect a to be bigger than b, which means (a - b) is a positive number. And if the defender is more skilled, we expect b to be bigger than a and (a - b) to be a negative number.
(a - b) |
Δ1+ |
Δ2+ |
Δ3+ |
Δ4+ |
Δ5+ |
Δ6+ |
Δ7+ |
Δ8+ |
Δ9+ |
|---|---|---|---|---|---|---|---|---|---|
| -10 | 0.69% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| -9 | 2.08% | 0.69% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| -8 | 4.17% | 2.08% | 0.69% | 0% | 0% | 0% | 0% | 0% | 0% |
| -7 | 6.94% | 4.17% | 2.08% | 0.69% | 0% | 0% | 0% | 0% | 0% |
| -6 | 10.4% | 6.94% | 4.17% | 2.08% | 0.69% | 0% | 0% | 0% | 0% |
| -5 | 14.6% | 10.4% | 6.94% | 4.17% | 2.08% | 0.69% | 0% | 0% | 0% |
| -4 | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% | 2.08% | 0.69% | 0% | 0% |
| -3 | 25% | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% | 2.08% | 0.69% | 0% |
| -2 | 31.3% | 25% | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% | 2.08% | 0.69% |
| -1 | 38.2% | 31.3% | 25% | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% | 2.08% |
| 0 | 45.8% | 38.2% | 31.3% | 25% | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% |
| +1 | 54.2% | 45.8% | 38.2% | 31.3% | 25% | 19.4% | 14.6% | 10.4% | 6.94% |
| +2 | 61.8% | 54.2% | 45.8% | 38.2% | 31.3% | 25% | 19.4% | 14.6% | 10.4% |
| +3 | 68.8% | 61.8% | 54.2% | 45.8% | 38.2% | 31.3% | 25% | 19.4% | 14.6% |
| +4 | 75% | 68.8% | 61.8% | 54.2% | 45.8% | 38.2% | 31.3% | 25% | 19.4% |
| +5 | 80.6% | 75% | 68.8% | 61.8% | 54.2% | 45.8% | 38.2% | 31.3% | 25% |
| +6 | 85.4% | 80.6% | 75% | 68.8% | 61.8% | 54.2% | 45.8% | 38.2% | 31.3% |
| +7 | 89.6% | 85.4% | 80.6% | 75% | 68.8% | 61.8% | 54.2% | 45.8% | 38.2% |
| +8 | 93.1% | 89.6% | 85.4% | 80.6% | 75% | 68.8% | 61.8% | 54.2% | 45.8% |
| +9 | 95.8% | 93.1% | 89.6% | 85.4% | 80.6% | 75% | 68.8% | 61.8% | 54.2% |
| +10 | 97.9% | 95.8% | 93.1% | 89.6% | 85.4% | 80.6% | 75% | 68.8% | 61.8% |
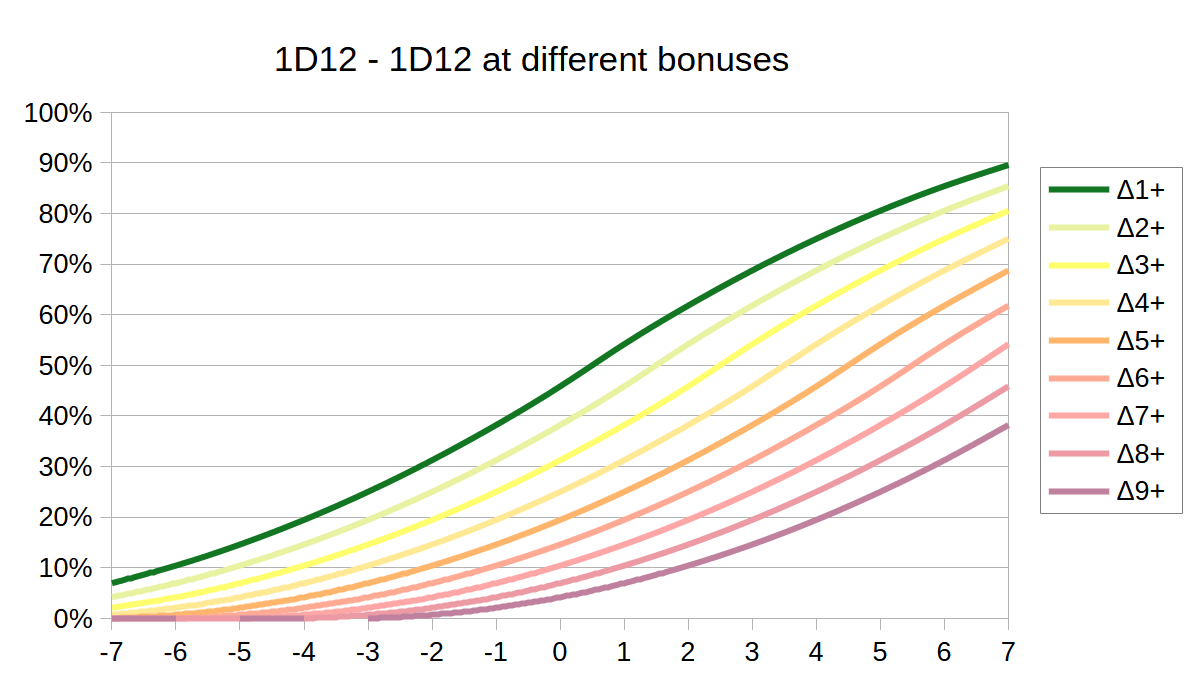
Δ1+ here means the chance of getting a difference of one or higher. The column Δ2+ shows the chance of getting a difference of 2 or higher. More information on how to calculate these cumulative percentage chances can be fond in the previous post: Die Rolls. Take mental note of how these numbers got more headroom upwards, then they got downwards - we are going to make use of that headroom later, when we introduce different categories of armor.
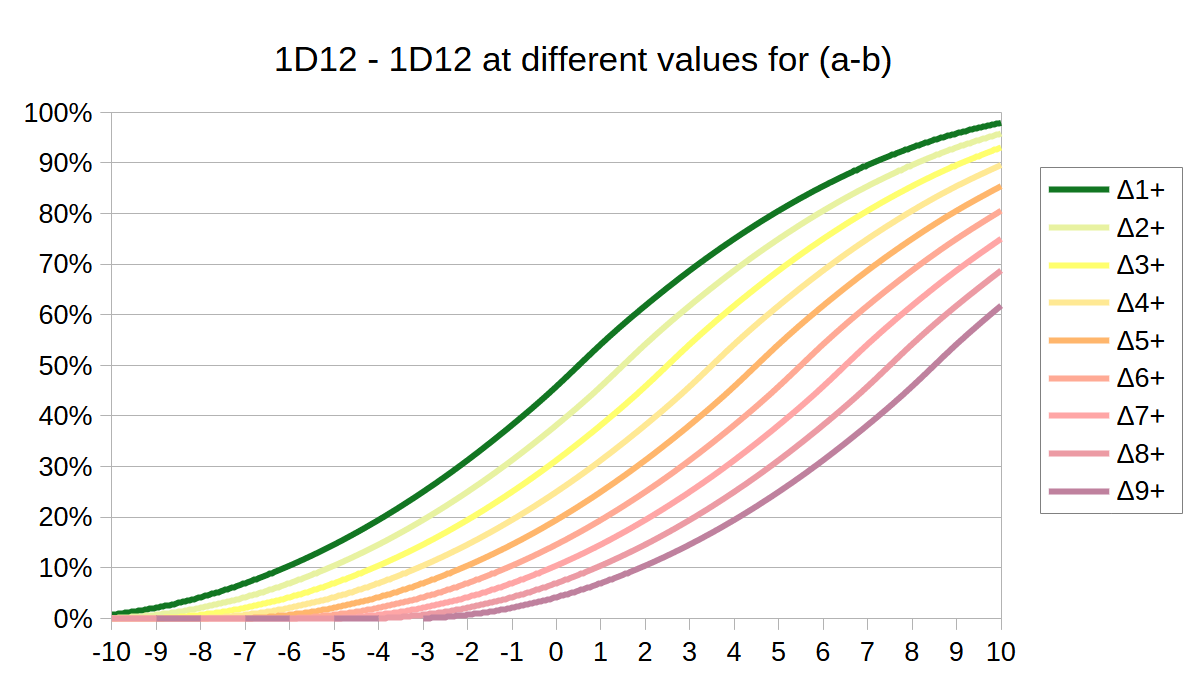We are mainly interested in that dark green line of Δ1+ - which represents our chance to hit.
We get a nice sigmoidal curve there for Δ1+ - which is of course exactly what we would expect when doing cumulative numbers on a bell shaped distribution (no worries - we won’t have to actually calculate any integrals or derivatives - we just can see them happen in the graphs). Our two D12s aren’t actually on a bell-shaped curve, but have this pyramid shape which is only a rough approximation of a bell curve. But as we can see here, it’s close enough to give us the desired end result, because this sigmoidal curve is exactly what we want.
If you look closely at the values in the table, you will see that going from +0 to +1 gives us the expected increase of +8.33% in chance (rounding errors not withstanding) - but when going from +9 to +10 that same +1 bump gives us only a +2.1% increase in chance. It’s exactly this diminishing returns effect, that will allow us to achieve our goal - but we do need more of it. The effect is not quite strong enough quite yet.
Diminishing Returns
Instead of plugging the attack bonus a and the armor class b into our formula directly - we can calculate (a-b) ahead of time, and then get a bonus for the die roll. To get the bonus that matches any given (a-b) we can use a table to look it up. This does allow us, to add even more diminishing returns on top of what we already have. It also allows us to easily cap the actual bonus that’s added to the die roll.
Let’s use the triangular numbers for that purpose. These are a great fit, adding just the right amount of additional diminishing returns. (They also happen to apply to the point-buy system I want to use later).
Diminishing Returns Table (DRT)
(a-b) |
0 | 1 | 2-3 | 4-6 | 7-10 | 11-15 | 16-21 | 22+ |
|---|---|---|---|---|---|---|---|---|
| Bonus | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Yes, this is an extra rule for adding more diminishing returns on top of what we naturally have. I feel that in this case, the pay-off is worth the added complexity.
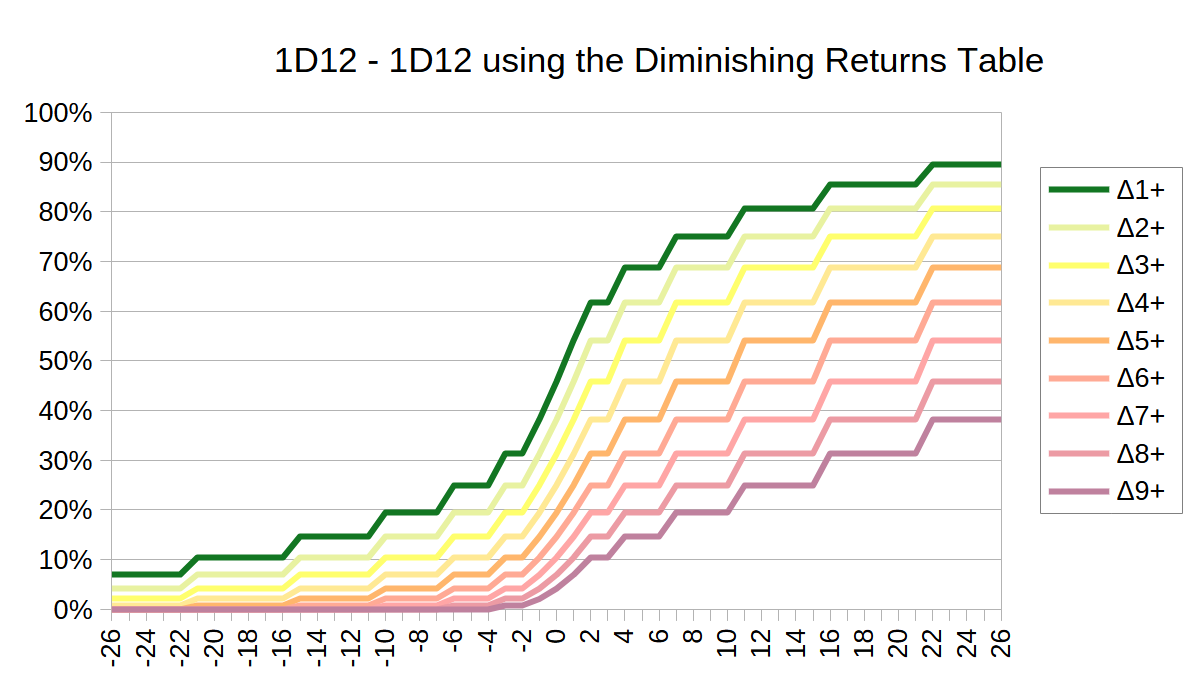All lines continue straight out to negative infinity on the left, as well as positive infinity on the right
We now are getting steps in our graph, but these are not noticable to the player. The players don’t have to add multiple +1s to their attack rating before they get any result, because this is not applied to their attack rating alone. Instead it is applied to the difference of their attack rating minus the enemy’s defense rating - and depending on what the enemy’s defense rating is, any +1 could be the one that gets you up the next step. More importantly though, going from 0 to 1, or from 1 to 2 will always have an effect - it’s only at higher differences that a single step up only happens to half or a third of the enemies.
Up until now, I have been calling
aandban “attack bonus” and “armor class” respectively. These are the terms most people are familiar with from D&D and the many D&D-likes out there. But now that we are using the DRT, we are no longer applying these as a bonus to the die roll. Instead we use these to look up the bonus in the table.That’s why going forward, I will be calling
athe “attack rating”, rather than a bonus. AndbI will be calling the “defense rating” for consistency - but the character skill that provides this “defense rating” is actually going to be called “evasion”. We are not going to have any armor class in this combat system, as armor is going to provide damage reduction rather than AC.
We can also see, that our chances to land a Δ9+ (basically a critical hit) becomes 0% at a difference of -4. Δ8+ hits become 0% at -7. Δ7+ hits at -11. This means that the damage potential of a many-shot weapon is getting increasingly reduced against opponents of higher skill levels. This increases the survivability of stronger characters in a very natural fashion - no increase in hit points required. At the same time it allows characters at higher skill levels to deal more damage overall to lower opponents - again without having to add any bonus to damage. All of this also helps make the outcome of fights somewhat more predictable - but without completely removing the risk for the more skilled character.
Between the diminishing returns and the built-in cap at a +7/-7 bonus, strength in numbers stays mostly intact. A +20 character will totally trounce a single +2 enemy - but will probably stand little chance against 10 of them. A +6 character should have a fairly good chance of defeating a single +2 - but might struggle against two ot them. We will have to work out all the rules and then run some mock fights to get definite numbers on this - but this is roughly the ballpark we expect.
Looking up the DRT is the job of the GM. It’s easy to move the bonus from the attacker side to the defender sidy, by simply flipping the sign in front (from positive to negative or vice versa). This allows the GM to always keep the bonus on the enemy roll, and never tell the number to the player. This way, the players can’t pin down what the enemy’s actual attack and defense ratings are.
This also makes things very easy for the players - who only have to roll a single die and are done. But it does mean some extra work for the GM, who has to look up all the bonuses. These don’t change - so he can keep reusing the bonus in future turns, but he does need to look it up at least once for each character and enemy that are attacking each other. That is a downside - but this is the only look-up table we need during combat, and it’s a very small one.
Conclusion
We now have a basic system where more skilled opponents are noticably more effective than less skilled ones - but things do not get ridiculous as the skill gap increases. Strength in numbers is preserved. There are strong diminishing returns effects to reign things in. All of that works organically by just changing attack rating and defense rating, without the need to increase hit points or damage bonuses or anything else.
We also have a system that allows for great weapon diversity. Some will only reach their full damage potential when landing many hits, while others will not not be reliant on that. Some will be more affected by armor strength than others. Different weapons will shine in different situations.
And armors are a trade-off between defense rating (making you harder to hit) and damage reduction (reducing the damage you take from hits). Oh wait, they aren’t quite yet - we still have to work that out!
Armor and Evasion
We want to have 3 main categories of armor: light, medium and heavy - which are fundamentally different from each other. We do of course also want multiple armor types per category - but the differences between those don’t have to be fundamental.
The Levers We Can Pull
Our main characteristics for armor are defense rating (take less hits) and damage reduction (take less damage when hit). Light armors should have high defense rating (which we are going to call “evasion”) and low damage reduction, while heavy armors shall have low evasion and high damage reduction. That will result in natural strengths and weaknesses - depending on the situation and the weapons opponents use. Medium armor should be average in both characteristics and have neither the strengths nor the weaknesses of the others, making it a good allround choice.
For the sake of keeping numbers as small and easy to handle as possible, damage reduction values should probably be 1, 2 and 3 - or maybe even 0, 1 and 2. This does of course also influence the damage numbers that weapons should have. We won’t be able to nail down these numbers until we work out both armors and weapons in full detail - which isn’t going to happen in this post.
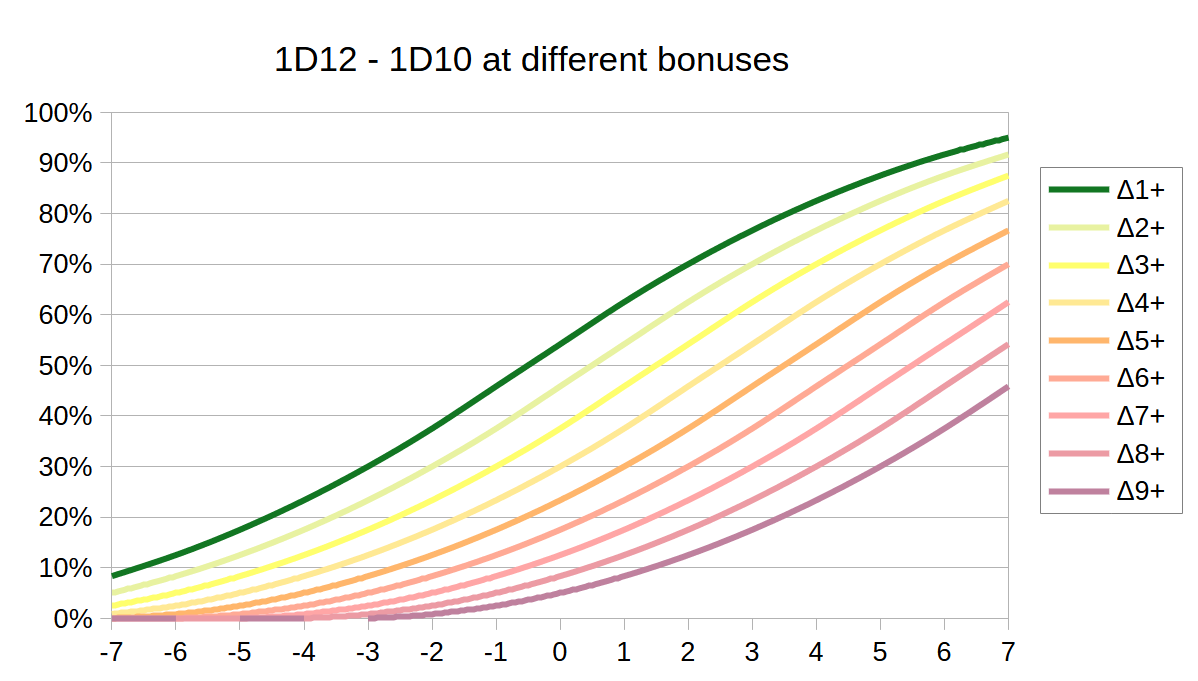
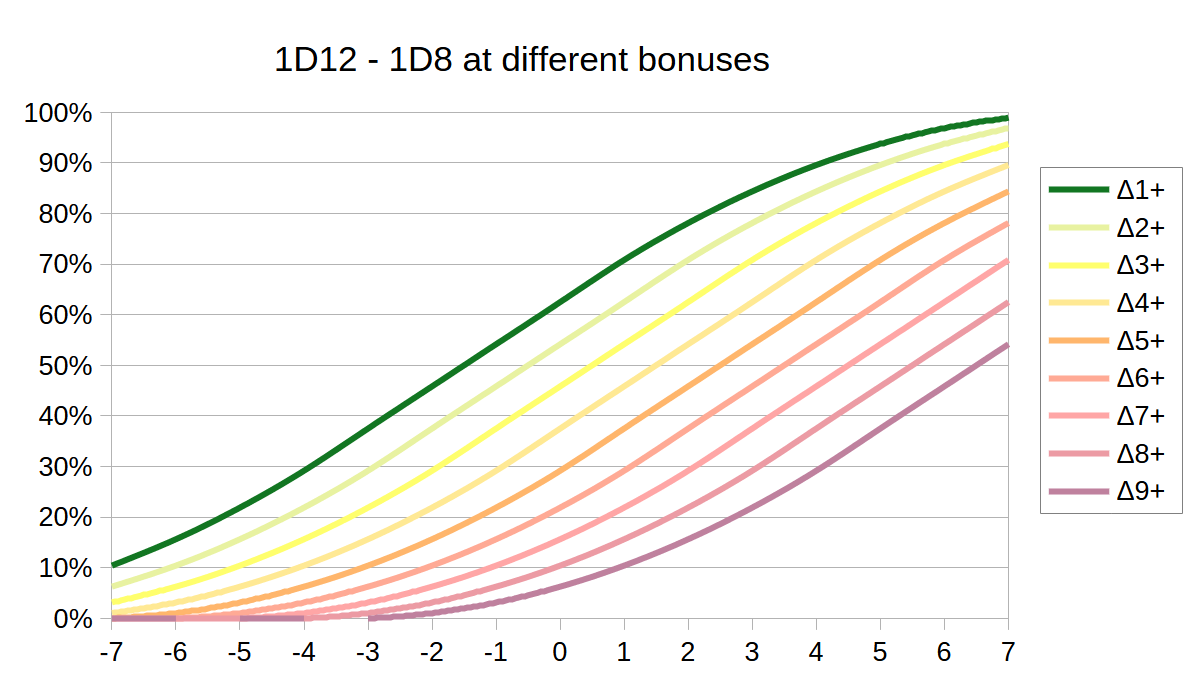
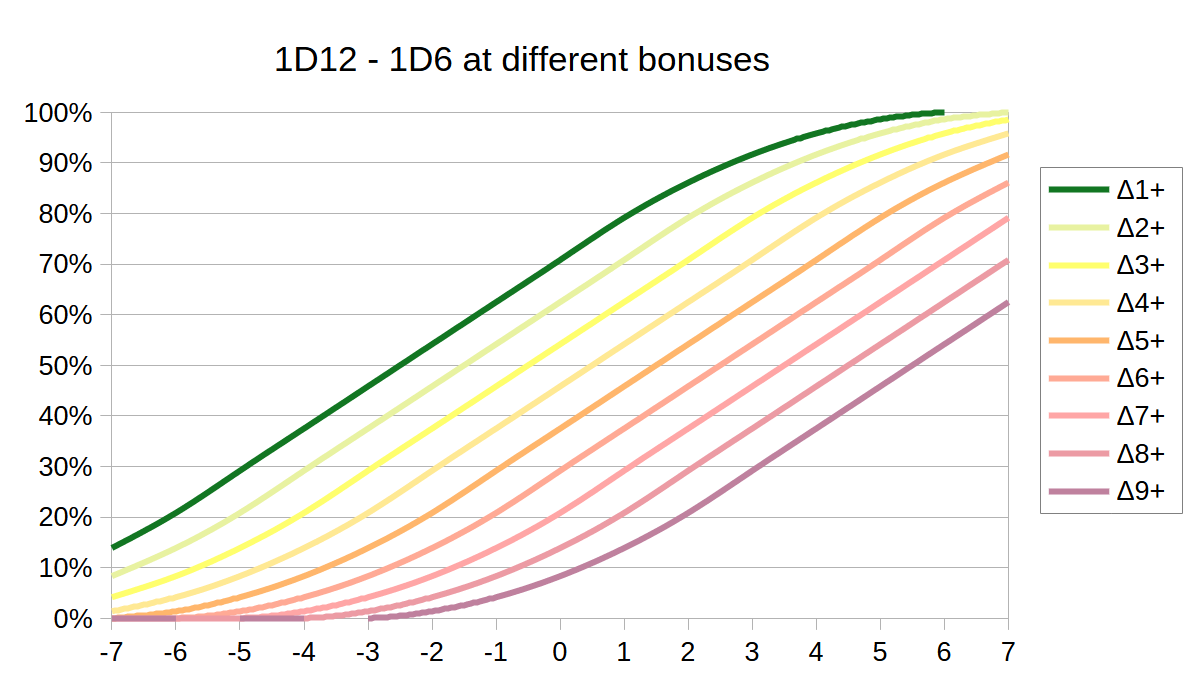
I have already mentioned that players will be able to improve their attack rating by spending XP. Exactly the same is going to be true for defense rating (and we’re going to call that “evasion”) - thus divorcing the defense rating from armor. But we still want armor to balance evasion against damage reduction - but I don’t want armor to give you +X evasion. There’s a more elegant way, and that is to have armor give you a different die size for your evasion roll instead. So, your training level in the evasion skill defines your defense rating - and the armor provides the die to roll. Either light armor = D12, medium armor = D10, heavy armor = D8 - or light armor = D12, medium armor = D8, heavy armor = D4. Whatever gives us the best results.
In the final system, I’m probably not going to use the terms “attack rating” and “defense rating” at all. It’s going to be the attacker’s pistol skill (or rifle skill) against the defenders evasion skill. But when talking in a generalized manner - independent of such implementation-specifics - “attack rating” and “defense rating” are the more descriptive terms.
A Closer Look At The Numbers
| Die | Δ1+ |
Δ2+ |
Δ3+ |
Δ4+ |
Δ5+ |
Δ6+ |
Δ7+ |
Δ8+ |
Δ9+ |
|---|---|---|---|---|---|---|---|---|---|
D12 |
45.8% | 38.2% | 31.3% | 25% | 19.4% | 14.6% | 10.4% | 6.94% | 4.17% |
D10 |
54.2% | 45.8% | 37.5% | 30% | 23.3% | 17.5% | 12.5% | 8.33% | 5% |
D8 |
62.5% | 54.2% | 45.8% | 37.5% | 29.2% | 21.9% | 15.6% | 10.4% | 6.25% |
D6 |
70.8% | 62.5% | 54.2% | 45.8% | 37.5% | 29.2% | 20.8% | 13.9% | 8.33% |
D4 |
79.2% | 70.8% | 62.5% | 54.2% | 45.8% | 37.5% | 29.2% | 20.8% | 12.5% |
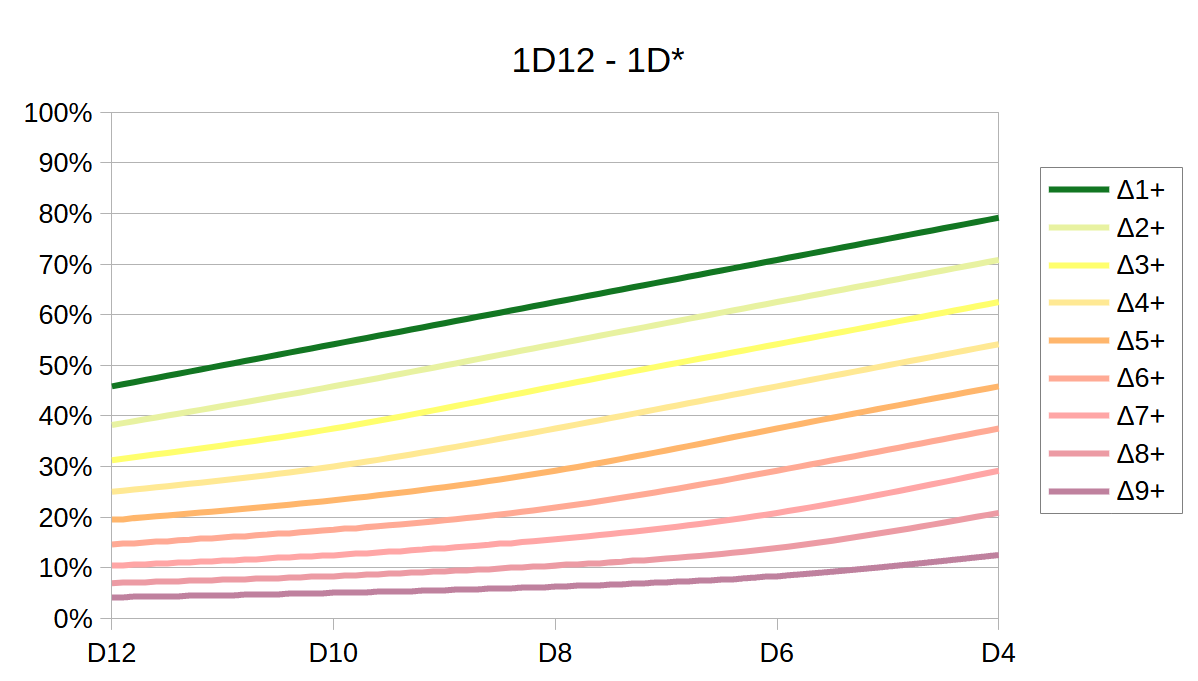Looking at it one way - nothing unexpected
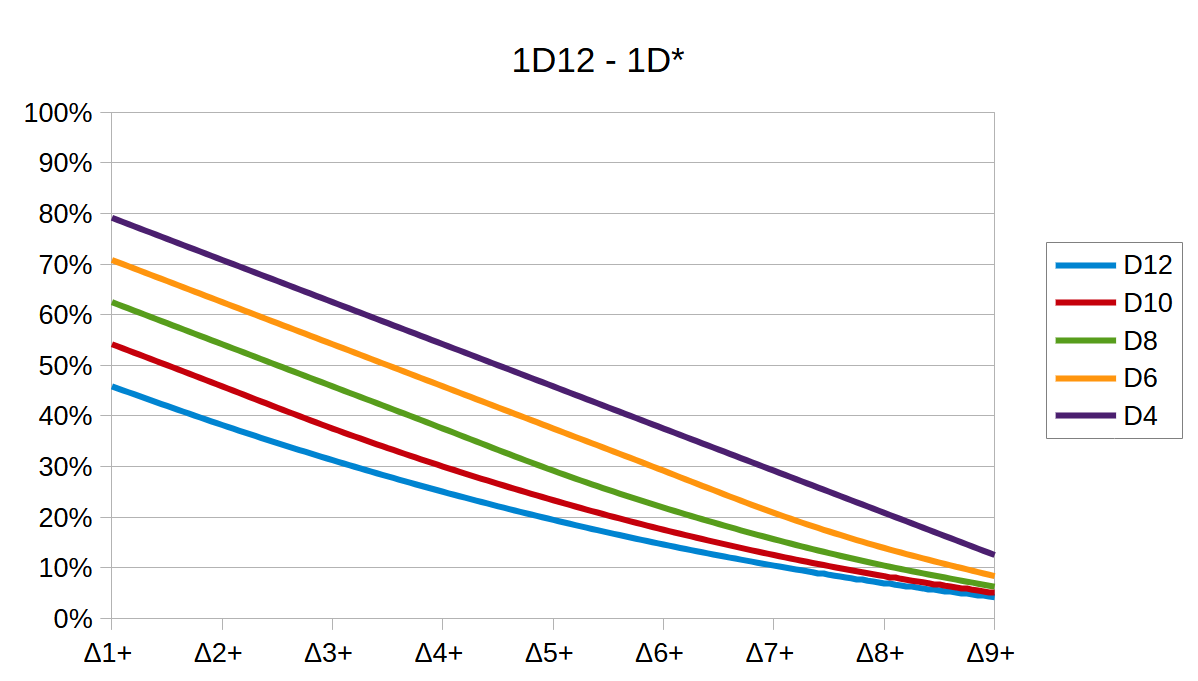Looking at it the other way - same thing
Base chance to hit goes from roughly 46% for light armor, up to roughly 80% for heavy armor when using D4. Chance to land a Δ9+ crit goes from roughly 4% to roughly 12% - almost three times as much. Heavy armors are going to take more hits more often.
When facing a 9-shot weapon, on total average, a D12-evasion armor would expect to take 2 hits, a D10 armor 2.3 hits, a D8 armor 2.8 hits, a D6 armor 3.4 hits, and a D4 armor 4.1 hits. When facing a 1-shot weapon, the lighest armor would expect 0.5 hits and the heaviest 0.8 hits. Overall the heaviest armor would be taking roughly twice as many hits as the lightest one. In practice the effect would be even more pronounced, as wearers of light armor are more likely to invest XP in their evasion skill, while wearers of heavy armors are probably gonna rely more on their high damage reduction - rather than evasion.
So far, these numbers and graphs were for equal opponents. Let’s also look at the effects this has on opponents of differing skill levels. Now we are finally starting to make use of that available headroom!
We see, that against the D6 armor at +7 bonus reaches a 100% chance to land one hit - but still has less than 100% chance of landing two. So, at that skill gap, you are guaranteed to do at least minimum damage - as you cannot miss. That’s still perfectly fine - we are trying to avoid 100% chances - but this is not a 100% chance to do full damage. (Except for sniper weapons - then it is!). We now have run out of headroom though!
Against the D4 armor an attacker at +7 bonus gets 4 guaranteed hits and has a 70% chance to land a Δ9+ crit. That sounds bad. That might just be too much. Yes this only happens when basically a max level character fights against a min level one - but even at a significantly lower power gap, it’s still three or two guaranteed hits, and 60% or 50% for a Δ9+ crit.
So, maybe we have to limit bonuses at +6 instead of +7. Or maybe we can’t use D4 armor at all, and should stick to either D12, D10, D8 - or maybe we should try D10, D8, D6. That is gonna require some play-testing to figure out.
I want to explicitly point out, that these graphs and numbers are not meant to replace play-testing, but to be additional input on top of that.
You can’t calculate fun. Even with all the numbers and understanding of the math, we are still relying on gut-feeling for what is and isn’t fun. And it is possible to find the fun, using experience and gut feeling alone (through blind trial and error) - without looking at any numbers at all. But it is not possible to do so just by the numbers, and without play-testing.
Understanding how the numbers work still does give you a deeper understanding, more data points you can develop a gut-feeling for, and will ultimately allow you to make more informed decisions. I also find it quite fascinating!
Resulting Options
We now have a range of possible base armor-sets that we can try out for further testing:
| Armor Set 1 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 0 | 1 | 2 |
| evasion die | D12 |
D10 |
D8 |
| Armor Set 2 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 0 | 1 | 2 |
| evasion die | D10 |
D8 |
D6 |
| Armor Set 3 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 0 | 1 | 2 |
| evasion die | D12 |
D8 |
D4 |
| Armor Set 4 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 1 | 2 | 3 |
| evasion die | D12 |
D10 |
D8 |
| Armor Set 5 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 1 | 2 | 3 |
| evasion die | D10 |
D8 |
D6 |
| Armor Set 6 | light | medium | heavy |
|---|---|---|---|
| damage reduction | 1 | 2 | 3 |
| evasion die | D12 |
D8 |
D4 |
Which one do you think has the most potential? My gut feeling just stirred, and made me excited for Set 7:
| Armor Set 7 | stealth | light | medium | heavy |
|---|---|---|---|---|
| damage reduction | 0 | 1 | 2 | 3 |
| evasion die | D12 |
D10 |
D8 |
D6 |
Heck, we could even try doing Set 8 - if we can somehow manage to accomodate such high damage reduction:
| Armor Set 8 | stealth | light | medium | heavy | power |
|---|---|---|---|---|---|
| damage reduction | 0 | 1 | 2 | 3 | 4 |
| evasion die | D12 |
D10 |
D8 |
D6 |
D4 |
I am of course assuming here, that both “stealth” and “power” armor are special in a way and don’t follow the same pattern as light/medium/heavy. Just adding even lighter and even heavier armor would just needlessly blur the lines between light and lighter, as well as heavy and heavier. These additional armors have to stand out in other ways - which gives us more options to deal with that D4 isse on the power armor.
But there is a real chance, that D10, D8 and D6 just don’t feel distinct enough - and that we do have to fall back to D12, D8 and D4 to achieve greater separation and differentiation - forcing us to find another way to mitigate that 100% problem with the D4. We will see.
But in order to actually figure that out, we are also going to need a base set of Weapons to test against.
Weapon Damage And Firing Rate
We can have weapons firing anywhere from one to nine shots. That cut-off at nine is not just to keep things simple and single-digit - but also because the chance of landing Δ9+ hits get too miniscule. If we assume evasion D8 and damage reduction 2 to be our “average” armor, then we got a base chance of roughly 6% to land a Δ9+. That’s very similar to the 5% chance of landing a crit on a natural 20, found in many other systems.
Landing 9 hits is not going to be common. But landing 4 or 5 hits (which would be the amount of shots the average weapon fires) is gonna be a regular occurence.
A Closer Look At The Numbers
Let’s see how much average total damage weapons with various numbers for shots and damage would do, against our standard armor with damage reduction 2:
| Weapons | 1 shot | 2 shots | 3 shots | 4 shots | 5 shots | 6 shots | 7 shots | 8 shots | 9 shots |
|---|---|---|---|---|---|---|---|---|---|
| 1 damage | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 damage | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 damage | 0.6 | 1.2 | 1.6 | 2.0 | 2.3 | 2.5 | 2.7 | 2.8 | 2.8 |
| 4 damage | 1.3 | 2.3 | 3.3 | 4.0 | 4.6 | 5.0 | 5.3 | 5.5 | 5.7 |
| 5 damage | 1.9 | 3.5 | 4.9 | 6.0 | 6.9 | 7.5 | 8.0 | 8.3 | 8.5 |
| 6 damage | 2.5 | 4.7 | 6.5 | 8.0 | 9.2 | 10.0 | 10.7 | 11.1 | 11.3 |
| 7 damage | 3.1 | 5.8 | 8.1 | 10.0 | 11.5 | 12.6 | 13.3 | 13.9 | 14.2 |
| 8 damage | 3.8 | 7.0 | 9.8 | 12.0 | 13.8 | 15.1 | 16.0 | 16.6 | 17.0 |
| 9 damage | 4.4 | 8.2 | 11.4 | 14.0 | 16.0 | 17.6 | 18.7 | 19.4 | 19.8 |
| 10 damage | 5.0 | 9.3 | 13.0 | 16.0 | 18.3 | 20.1 | 21.3 | 22.2 | 22.7 |
| 11 damage | 5.6 | 10.5 | 14.6 | 18.0 | 20.6 | 22.6 | 24.0 | 24.9 | 25.5 |
| 12 damage | 6.3 | 11.7 | 16.3 | 20.0 | 22.9 | 25.1 | 26.7 | 27.7 | 28.3 |
| 13 damage | 6.9 | 12.8 | 17.9 | 22.0 | 25.2 | 27.6 | 29.3 | 30.5 | 31.2 |
| 14 damage | 7.5 | 14.0 | 19.5 | 24.0 | 27.5 | 30.1 | 32.0 | 33.3 | 34.0 |
| 15 damage | 8.1 | 15.2 | 21.1 | 26.0 | 29.8 | 32.6 | 34.7 | 36.0 | 36.8 |
Let’s look at just the area of 3 to 6 shots for now. Those will be our common, regular weapons. We will also have a 1-shot sniper weapon, and probably some 8 shot or 9 shot shot-gun-style weapon - but those are gonna require special treatment. Let’s focus on the non-specials for now.
If we want average damage to be as balanced and equal as it can be, we could go with:
| shots | damage per shot | average damage | max damage potential | |
|---|---|---|---|---|
| (Weapon 1) | 2 | 12 | 11.7 | 20 |
| Weapon 2 | 3 | 9 | 11.4 | 21 |
| Weapon 3 | 4 | 8 | 12.0 | 24 |
| Weapon 4 | 5 | 7 | 11.5 | 25 |
| Weapon 5 | 6 | 6 | 10.0 | 24 |
| (Weapon 6) | 7 | 6 | 10.7 | 28 |
… but do we actually want completely equal balance?
Maybe we want damage potential to increase the more shots are fired:
| shots | damage per shot | average damage | max damage potential | |
|---|---|---|---|---|
| (Weapon 1) | 2 | 7 | 5.8 | 10 |
| Weapon 2 | 3 | 7 | 8.1 | 15 |
| Weapon 3 | 4 | 7 | 10.0 | 20 |
| Weapon 4 | 5 | 7 | 11.5 | 25 |
| Weapon 5 | 6 | 7 | 12.6 | 30 |
| (Weapon 6) | 7 | 7 | 13.3 | 35 |
Maybe we want the opposite: for the damage potential to DEcrease the more shots are fired:
| shots | damage per shot | average damage | max damage potential | |
|---|---|---|---|---|
| (Weapon 1) | 2 | 14 | 14.0 | 24 |
| Weapon 2 | 3 | 10 | 13.0 | 24 |
| Weapon 3 | 4 | 8 | 12.0 | 24 |
| Weapon 4 | 5 | 7 | 11.5 | 25 |
| Weapon 5 | 6 | 6 | 10.0 | 24 |
| (Weapon 6) | 7 | 5 | 8.0 | 21 |
… but what do we actually want?
Further Considerations
We might want to balance those weapons to have roughly equal average damage overall - but we don’t really know yet. We also have to consider the following points:
- Armors will be equipped with energy shields, balanced by max shield points and recharge rates.
- Weapons will get different damage types, interacting differntly with armor and shields.
- Weapons strong against armor should be weak against shields, and vice versa.
- Melee weapons will exist and work mechanically slightly different than ranged weapons.
- Weapons will have different ranges - melee weapons work at close range only, regular weapons at close and medium range, sniper weapons at medium and long range.
- Some weapons will be strong against lower-skill enemies, and weak against higher skill ones - others will be more uniform in their damage potential.
For these different damage type and melee weapons to be different in a useful way, we will need some extra effects, like for example:
- Armor penetration
- Interrupting shield recharge (ion or e.m.p. weapons?)
- Variable damage (single shot weapons could use delta to determine damage instead of hits)
- Shield penetration (maybe?)
- Stun
- Knockdown
- Damage over time (poison, fire)
- Area of effect damage
- and more…
There’s a lot of different factors coming into play there - which is great, because this is exactly the depth and diversity we are aiming for. But this also going to be a major challenge to get right. Too much so to squeeze this into this already lengthy post.
Therefore, this will have to wait for a future installment - where we take a closer look at weapons, armors and shields.
Summary And Conclusion
Our combat system now works as follows:
- The player tells the GM which weapon skill they are using (attack rating).
- The GM calulates defense rating (monsters evasion skill) - attack rating (player’s weapon skill) - and looks up the bonus
- The GM rolls a D8 (depending on armor worn) and adds/subtracts the bonus, getting a result
- The player rolls a D12 and this is their result
- The GM calculates the delta: player’s result - the monster’s result and tells the player
- The player tells the GM how many hits that are (depending on how many shots the weapons fire) - and how much damage each hit does.
- The GM calulates (damage-per-hit - damage-reduction) * number-of-hits = total_damage_taken, and substracts that from the monsters hit points.
And the other way round:
- The GM tells the player they are being attacked by a monster
- The player tells the GM their evasion skill
- The GM calculates attack rating (monster’s weapon skill) - defense rating (player’s evasion skill) - and looks up the bonus
- The GM rolls a D12 and adds/substracts the bonus, getting a result
- The player rolls a D8 (depending on armor worn)
- The GM calculates the delta, and tells the player how many hits the monster made, at what damage per hit
- The player calculates (damage-per-hit - damage-reduction) * number-of-hits = total_damage_taken, and substracts that from their hit points
And we do know, that there will be a wide range of fairly different armors and weapons available, which have various strengths and weaknesses that balance each other out. Armors will have damage reduction and an evasion die, as well as energy shields with a max and a recharge rate. Weapon will have a number of shots fired, damage per hit and different damage types with different effects.
Many of the various strengths and weaknesses of these weapons and armors will emerge quite organically from very few written rules and even less rule exceptions. Diminishing returns will ensure that small differences in skill lead to noticeable results, but large differences in skill don’t break the game. The system works for arbitrarily high skill gaps, but anything past 22 points of difference has no further effect.
I believe what we have here is a fairly robust combat basis with fairly good potential!